Nuclear 01: How Nuclear Physics Works

A dive into the fundamentals of fission and fusion

Nuclear technology defies simple categorization. A single fission plant can power a city, and nuclear ships can circumnavigate the globe for twenty-five years between refueling. Yet the same materials that provide carbon-free power pose dangerous security risks.

Further, nuclear technology isn't one thing. Development approaches have diverged dramatically over the last eighty years. Different countries have adopted vastly different strategies driven by technical breakthroughs, resource constraints, sanctions, and public support — or lack thereof. Some countries even halted their nuclear efforts, while others steadily accelerated them.

Today, the industry is undergoing what may be a renaissance. Exploding datacenter demand is driving power needs skyward, while billions are pouring into fusion research. At the same time, fission plants are being exported around the world, creating sophisticated international dependencies and spheres of influence. Yet, the perceived and real dangers of nuclear persist. Chernobyl, Three Mile Island, and Fukushima are household names, and the possibility of weapons-grade uranium recently prompted airstrikes against Iran.

No other technology can both decarbonize entire electrical grids and destroy the cities it serves. It is this fundamental duality that makes nuclear technology uniquely complex to evaluate.

This essay is the first in a series that maps the nuclear landscape across physics, engineering, economics, and geopolitics. Beyond diving into nuclear technology, this series also serves a second purpose. It is a prototype for future As Built landscape series. I deliberately chose nuclear for the maiden voyage. It’s a topic I care deeply about, but to which I have no professional ties, which allows me to write independently.

Our main goal is to characterize the global fission market. To do this, we'll start with the core physics of nuclear reactions and how engineers harness them. We'll then examine the history of nuclear power and the policy decisions that shaped it, finally arriving at today's market. After all that, we'll repeat the process for fusion.

There are three types of nuclear reactions: fission, fusion, and decay. They're all fundamentally different processes, united by one fact: each transforms atoms into different elements.

Fission and fusion are common terms. Fission reactors power cities worldwide. Fusion research promises unlimited clean energy. Decay is less well known by name, but it's what makes materials radioactive. This essay unpacks how these three reactions work, forming the foundation of the series.

Atomic Structure

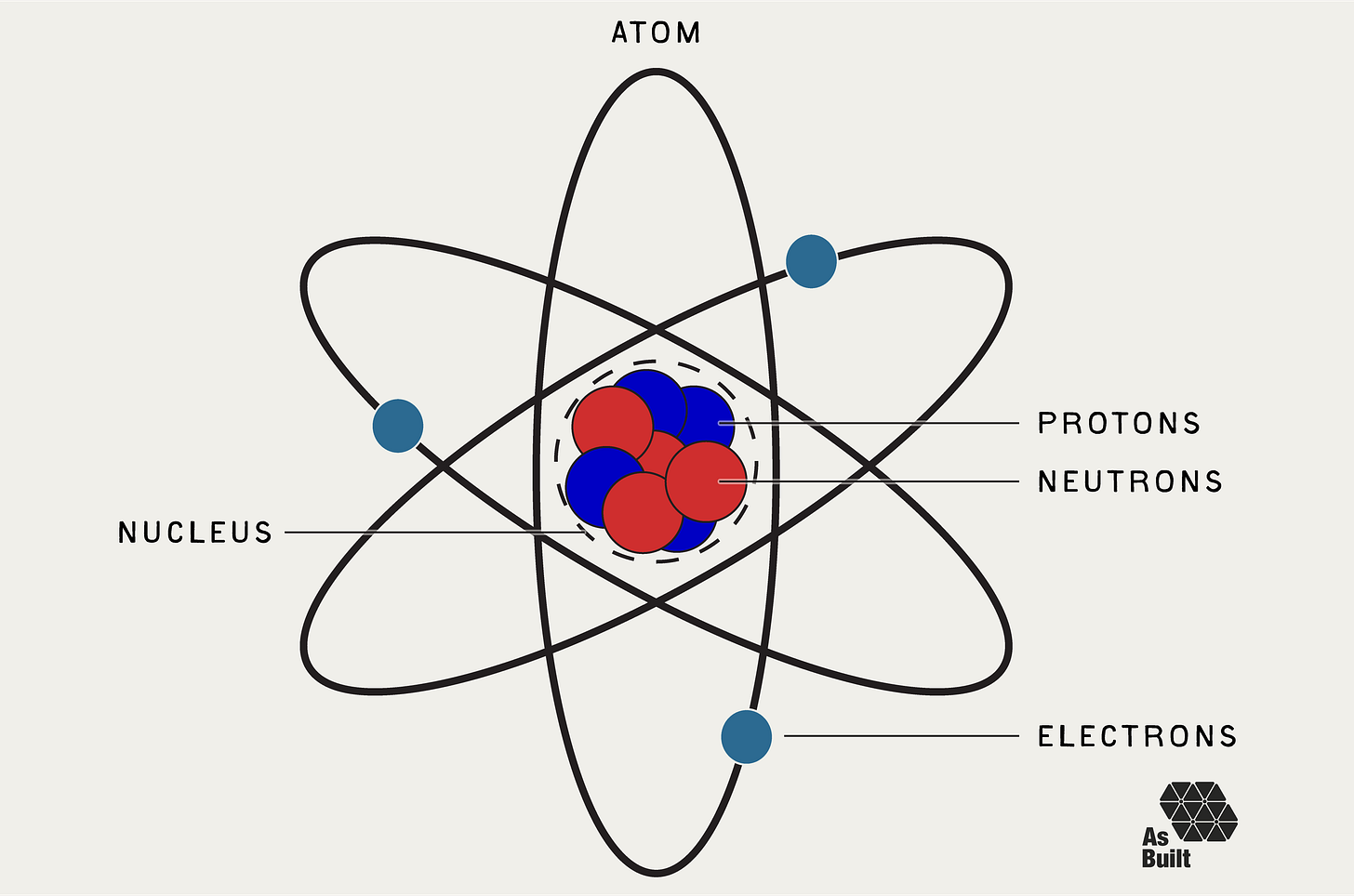
Since nuclear reactions transform atoms at their core, we first must understand the structure of an atom.

Atoms are the fundamental building blocks of all matter. At the center is a dense nucleus that packs together positively charged protons and neutral neutrons. Negatively charged electrons orbit the nucleus like satellites around Earth.

Each element on the periodic table is defined by a unique number of protons. Copper has 29 protons, hydrogen has one, and uranium has 92. Conversely, the number of neutrons can vary, and an atom's mass number is the total of its protons and neutrons.

Isotopes are atoms with the same number of protons but a different number of neutrons. Some isotopes are stable, while others are unstable and radioactively decay.

For example, carbon-12 has six protons and six neutrons, and is stable. Carbon-14 has six protons and eight neutrons, and is unstable. It undergoes radioactive decay with a half-life of approximately 5,730 years, making it helpful in determining the age of organic matter.

Chemical vs. Nuclear Reactions

We create more complex materials by combining atoms into molecules. Water (H₂O) consists of two hydrogen atoms and one oxygen atom. Steel is a mixture of iron, carbon, chromium, nickel, and other atoms. To make these materials, or break them apart, we use two types of reactions: chemical and nuclear.

Chemical reactions happen outside the nucleus. Atoms are rearranged by breaking and forming electron bonds. When gasoline burns, Carbon-hydrogen bonds break, and the atoms recombine with oxygen to form CO₂ and H₂O. Importantly, the atoms themselves don't change. Carbon stays carbon. Hydrogen stays hydrogen. Only the electron's configuration changes.

Nuclear reactions happen inside the nucleus. We don't rearrange atoms. Instead, we change the nucleus of the atom itself. That means changing the number or arrangement of protons and neutrons. These reactions include:

• One nucleus splitting into smaller pieces (fission)

• Two nuclei combining into one (fusion)

• A nucleus emitting particles and transforming (decay)

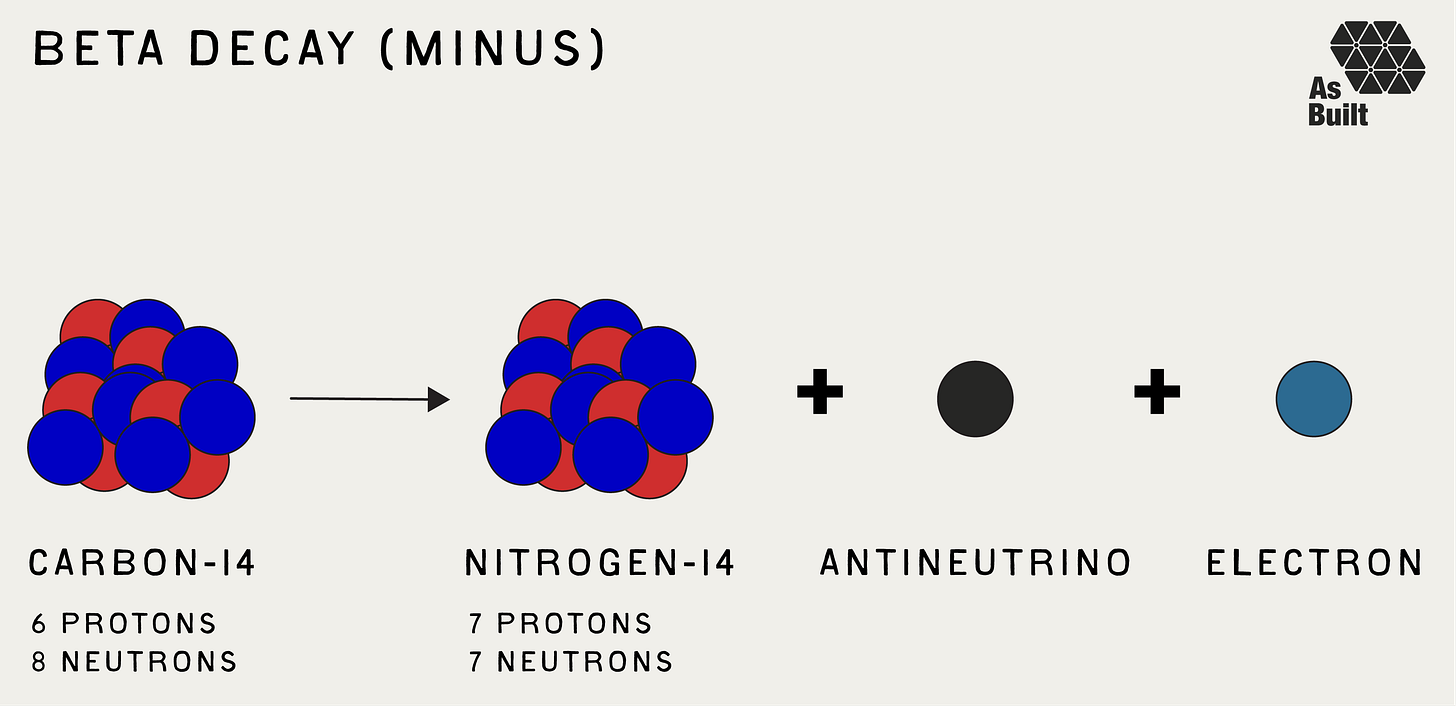
In all three, the atom's identity can change. In other words, it becomes something else. Going back to the carbon example, when carbon-14 decays, it emits an electron, and one neutron becomes a proton. Now with seven protons and seven neutrons, the atom has transformed into nitrogen-14.

As we'll see during fission, a uranium atom also changes its identity, splitting into different smaller atoms and releasing immense energy in the process.

Chemical Reactions

Before we examine nuclear reactions, chemical reactions help to establish a baseline for comparison, and let's consider how they generate energy.

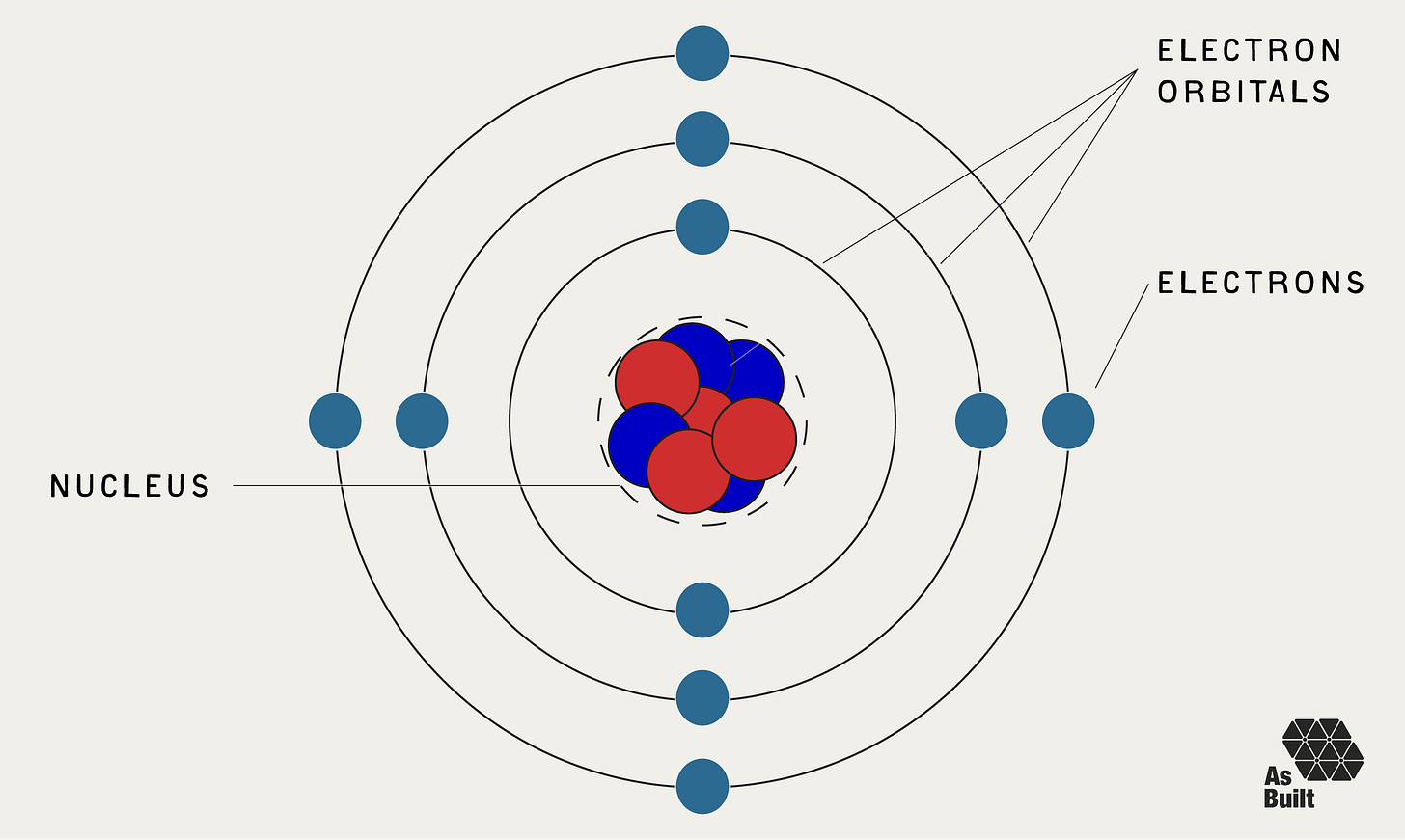
As electrons orbit the nucleus, they do so in different defined energy levels. Known as orbitals, each has a specific amount of potential energy. Generally, electrons closer to the nucleus are more tightly bound, while those in higher orbitals are more available for bonding.

When atoms form a chemical bond, electrons from different atoms interact, often by occupying a shared orbital between the nuclei. This lowers the overall energy of the system and creates a stable bond.

• Forming a bond releases energy, as electrons drop into a lower-energy orbital.

• Breaking a bond requires energy since we're pulling electrons away from a low-energy, shared state.

• Net energy is generated by breaking high-energy bonds and then forming low-energy bonds. The difference in energy is released as heat.

For example, in gasoline molecules, carbon and hydrogen atoms share electrons in stable C-H and C-C bonds, which store chemical energy. During combustion, these bonds break and the atoms form new, lower-energy bonds with oxygen, forming CO₂ and H₂O and releasing the energy difference as heat.

Chemical bonds vary in strength, but most lie in a range of 1–5 electron-volts (eV) per bond. For example, it takes about 4.3 eV to break a hydrocarbon (C-H) bond.

In reactions like combustion, dozens of bonds are broken and reformed per molecule. One kilogram of gasoline roughly contains 44 megajoules of chemical energy. Keep this baseline in mind as we consider nuclear reactions.

Nuclear Reactions and Binding Energy

Nuclear reactions alter the nucleus of the atom, rather than rearranging the electrons. This releases immense energy. Counterintuitively, we can release energy both by splitting heavy nuclei and combining light ones. The concept of binding energy will explain this phenomenon.

Our starting point is Einstein's famous E = mc² equation, which demonstrates that mass and energy are interchangeable. A small amount of mass (m) can be converted into an enormous amount of energy (E) because the speed of light (c) is a large number, and it's squared in the equation.

Applying this practically, when protons and neutrons bind together to form a nucleus, the resulting nucleus has slightly less mass than the sum of its individual parts. This missing mass has been converted to energy. Specifically, it is the binding energy that holds the nucleus together. It’s the energy required to pull a nucleus apart into individual protons and neutrons. It's also the energy released when a nucleus is assembled from those constituents.

For example, when two protons and two neutrons come together to form a helium nucleus, the individual masses add up to 4.0331 atomic mass units (amu), but a helium nucleus has a mass of only 4.0026 amu. The difference, 0.0301 amu, has been converted to 28.3 million electron volts (MeV) of binding energy.

Compare this 28.3 MeV to the 4.3 eV from a hydrocarbon chemical bond. It's 6.5 million times more energy. This comparison isn’t quite apples-to-apples, but it illustrates the different orders of magnitude of energy levels between the chemical and nuclear regimes.

The Binding Energy Curve

Here's where nuclear physics gets interesting. The amount of binding energy isn't the same for all nuclei. Some are bound much more tightly than others. This variation explains why fission and fusion can both release energy.

We usually think about binding energy per nucleon — that is, how much energy is required (or released) per proton or neutron in the nucleus. The more tightly bound the nucleons are, the lower the potential energy and the more stable the nucleus.

Plotting binding energy per nucleon versus mass number reveals a distinct trend. The binding energy per nucleon increases rapidly for light elements, peaks around iron-56 and nickel-62, then gradually decreases for heavier atoms. Elements at the peak are most tightly bound. It takes the most energy to pull them apart. The most stable nuclei sit at the peak, and everything else wants to get there.

• The fusion regime is to the left of the peak. Light nuclei, like hydrogen, are weakly bound. They fuse together to create heavier nuclei, like helium, and move up the curve. The resulting nucleus has a higher binding energy per nucleon, and that difference is released as energy.

• The fission regime is to the right of the peak. Heavy nuclei, like uranium-235, are also relatively loosely bound. When they split into smaller nuclei that are closer to the peak, these products are more tightly bound. The difference in binding energy per nucleon is released as energy.

In both cases, we're moving towards a more tightly bound, stable state. Energy can be released both by building up small nuclei or breaking down big ones, as long as we're trending towards the peak of the curve.

Fission: Splitting the Atom

In fission, a heavy nucleus splits into multiple lighter nuclei, releases several neutrons, and produces a burst of energy. Naturally occurring fission is rare. In most cases, we need to induce it by bombarding a nucleus with a free neutron.

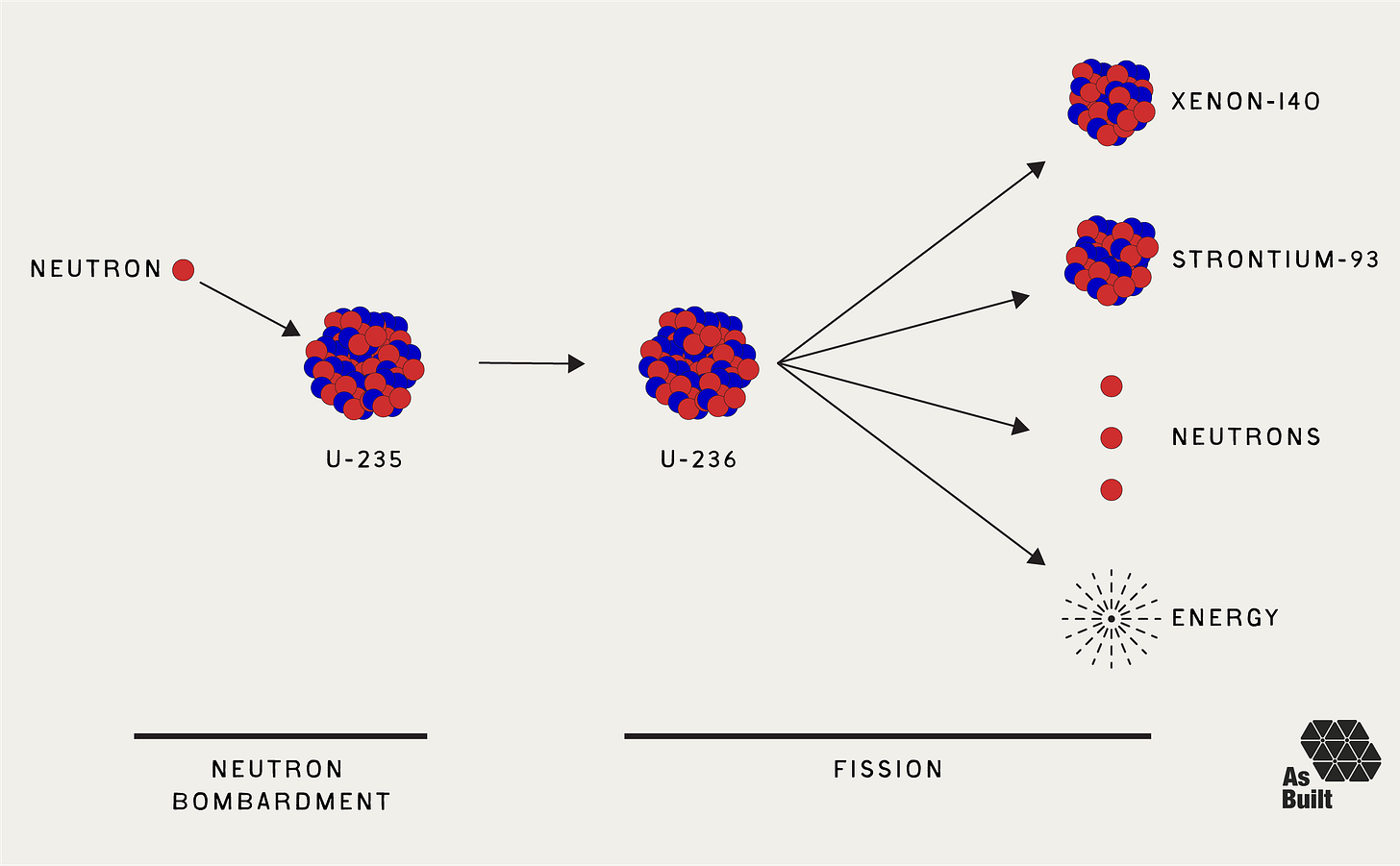
The most common fission process involves uranium-235 (U-235), which is a naturally occurring isotope with 92 protons and 143 neutrons. When a neutron collides with a U-235 atom, it's absorbed, forming uranium-236 (U-236). It's still uranium, but now with 236 total nucleons.

U-236 is unstable and rapidly undergoes fission, usually breaking into two smaller nuclei called fission products, plus additional neutrons, gamma radiation, and heat. The exact fission products vary probabilistically on a fission-by-fission basis. However, the quantity of nucleons and energy are conserved. Products can include barium, krypton, strontium, cesium, iodine, and xenon, among others.

Let's consider one possible example. Uranium-235 absorbs one neutron and becomes Uranium-236. This undergoes fission and splits into Xenon-140 and Strontium-93, while also releasing three neutrons and about 200 MeV of energy.

U-235 + neutron -> U-236 -> Xe-140 + Sr-93 + 3 neutrons + 200 MeV energy

Let's break down what happened here:

• We created fission products. Xenon-140 and strontium-93 are both radioactive isotopes. They're unstable and will decay over time. These fission fragments are commonly referred to as nuclear waste.

• We created three new free neutrons. Uranium-236 starts with 236 nucleons. Our fission products, xenon-140 and strontium-93, total 233 nucleons, leaving three free neutrons. These neutrons are essential. They can go on to cause further fission events, creating a self-sustaining chain reaction, which makes nuclear power possible.

• We released energy. Each fission event releases ~200 MeV of energy. It comes in a variety of forms, with an average breakdown of:

  • 80-85% kinetic energy from fission fragments

  • 2-3% kinetic energy from prompt neutrons

  • 3-4% prompt gamma radiation

  • 5-7% delayed beta/gamma from decay

  • ~5% lost to antineutrinos

Focusing on the kinetic energy, fast-moving fission products and neutrons travel through the solid fuel. They only make it microscopic distances as they collide with surrounding atoms, converting kinetic energy into heat. It is this heat that we subsequently capture and use to produce electricity.

Trillions of fission events happen per second. The sum of these represents the total amount of energy that is stored in uranium fuel. Theoretically, if all of our fuel were fissionable U-235 (which it's not), one kilogram would hold 82,000,000 MJ of energy.

However, pure U-235 fuel is not practical. Real uranium fuel contains mostly non-fissile U-238 isotopes, which significantly changes the energy density. Therefore, while commonly cited, the above value is theoretical and can be misleading when used for comparison purposes. Later, we’ll establish a framework for a more balanced approach to energy density comparisons.

Fusion: Building Bigger Atoms

Fusion is the second type of nuclear reaction. Two light nuclei combine to form a single, heavier nucleus and release energy in the process. Fusion can occur between many different nuclei. However, the most promising fusion reaction for energy generation involves combining two hydrogen isotopes:

• Deuterium (H-2): Hydrogen with one proton and one neutron

• Tritium (H-3): Hydrogen with one proton and two neutrons

Fusion's challenge is overcoming nature's fundamental forces. Recall that protons are positively charged, which means any two atomic nuclei naturally repel each other. Known as the Coulomb barrier, this is one of the primary obstacles to fusion. For two nuclei to get close enough for the strong nuclear force to take over and bind them together, they must collide with tremendous energy.

Creating the Conditions

Achieving such energy requires extreme conditions. Depending on the approach, this might be temperatures that exceed 100 million degrees Fahrenheit or pressures above 100 billion atmospheres. These conditions create plasma, which is a fourth state of matter where nuclei and electrons exist separately. Only in this plasma state can nuclei move fast enough to overcome their mutual repulsion.

These conditions don't exist naturally on Earth, and creating them is challenging. The plasma must be contained and controlled without any material walls, since no known material can withstand prolonged direct contact. This constraint has driven the development of two main approaches:

• Magnetic confinement traps plasma in invisible cages. Powerful magnetic fields, arranged in doughnut-shaped tokamaks or twisted stellarator ribbons, suspend plasma away from any physical walls. The challenge is maintaining this magnetic prison long enough for sustained fusion reactions, keeping the plasma hot and dense while it tries to escape in every direction.

• Inertial confinement compresses fuel faster than it can explode. Arrays of lasers focus enormous power onto fuel pellets smaller than peppercorns, heating and crushing them so rapidly that fusion ignites before the plasma can expand. The challenge is achieving uniformity and symmetry. Small timing or alignment mismatches let the pellet blow apart before fusion can run its course.

Energy Creation and Capture

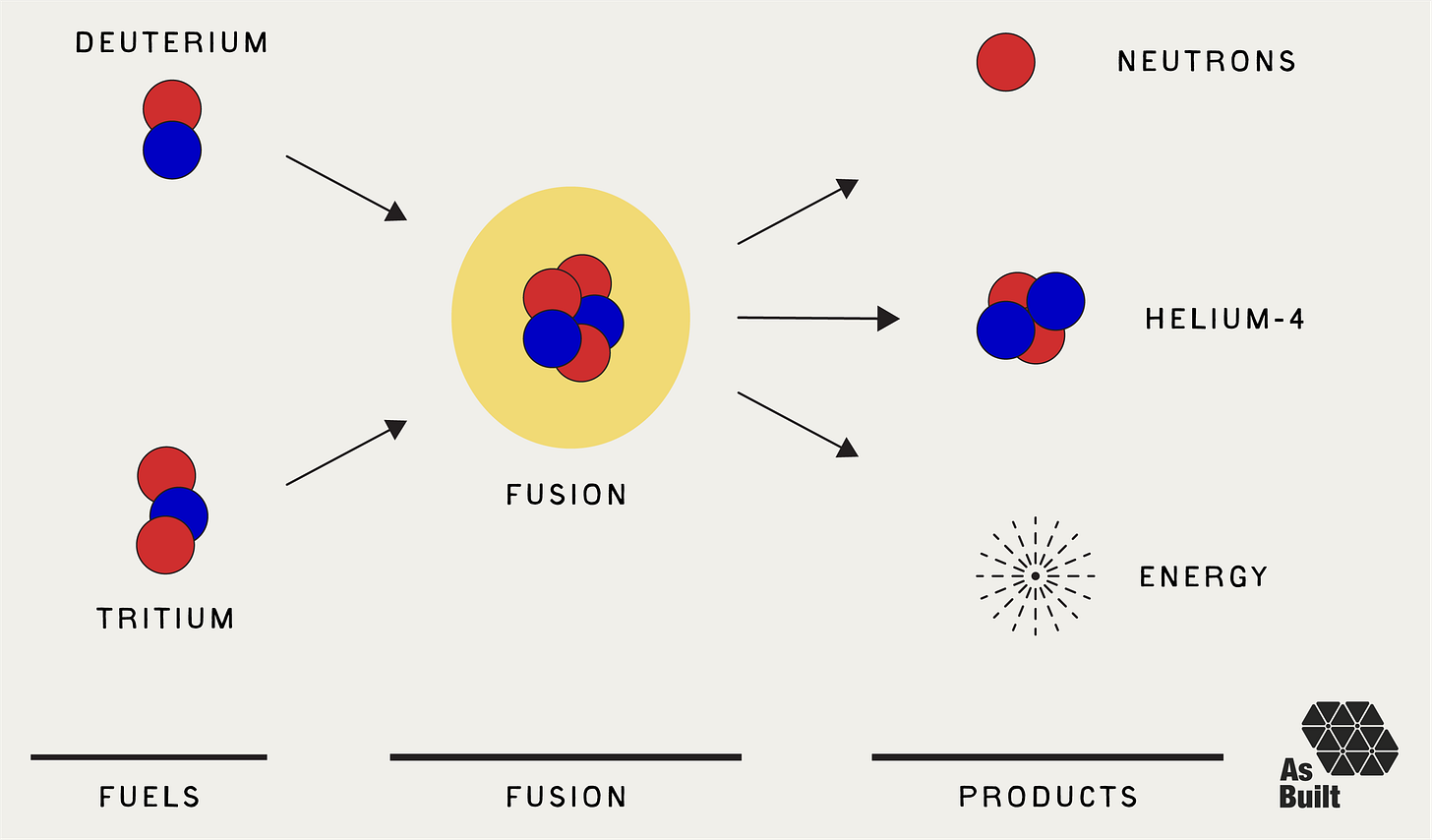
When deuterium and tritium nuclei collide with sufficient energy, they combine to create Helium-4. In the process, they expel one neutron and release about 17.6 MeV of energy.

H-2 + H-3 -> He-4 + 1 Neutron + 17.6 MeV

This might seem modest compared to the ~200 MeV from fission, but when normalized by nucleon mass, the power of fusion becomes apparent. The fusion reactants are much lighter (hydrogen instead of uranium). This results in high energy release on a per nucleon basis:

• Fusion: ~3.5 MeV per nucleon

• Fission: ~0.85 MeV per nucleon

On this basis, fusion releases about four times more energy than fission.

About 20% of the energy appears as kinetic energy of the helium nucleus. In magnetic confinement systems, this remains trapped by the magnetic fields used to contain the plasma.

The remaining 80% becomes kinetic energy of the fast neutron, which escapes the magnetic confinement entirely. These high-energy neutrons carry most of the fusion energy out of the plasma, where they similarly create heat, which can be captured for electricity production.

When scaled up to practical quantities, deuterium-tritium fuel has a theoretical energy density of roughly 340,000,000 MJ/kg. However, like with fission, inefficiencies and other considerations must be taken into account to compare energy densities.

Breeding Fuel

The neutrons also serve another crucial function. They breed more tritium fuel. Many fusion reactors are lined with lithium-6 blankets. When a neutron collides with a lithium-6 nucleus, it causes it to split into a tritium (H-3) atom and an alpha particle (equivalent to helium-4). Some energy is also released in the process.

Li-6 + neutron -> He-4 + H-3 + 4.8 MeV

This breeding process is essential because tritium doesn't exist naturally in significant quantities.

Deuterium, on the other hand, is naturally occurring, though in small quantities. Approximately 0.015% of seawater is composed of deuterium atoms, which can be concentrated and extracted. The ability to breed tritium in situ and general deuterium access gives fusion a sustainable fuel supply.

Fusion Today and Its Advantages

While fusion occurs naturally in stars, controlling it on Earth has proven extraordinarily difficult. Fusion has been achieved operationally in thermonuclear weapons, where a fission bomb creates the extreme conditions needed to trigger fusion reactions.

Harnessing fusion for power generation remains a development effort. International megaprojects like ITER compete with dozens of private fusion companies racing toward commercial viability. In the past few years, experiments have demonstrated that achieving net energy gain is possible, but scaling fusion to supply the electrical grid remains a work in progress.

Fusion's promise extends beyond just an energy advantage, and includes:

• Waste Stream: Fusion's primary byproduct is helium, an inert gas posing no storage concerns. Neutron activation of reactor components produces some radioactive waste, but this typically decays to safe levels within decades.

• Fuel Supply: Fusion fuels (deuterium and lithium for breeding tritium) are widely available.

• Safety: Fusion cannot experience a runaway reaction or meltdown. The extreme conditions required for fusion are inherently self-limiting. Any disturbance instantly stops the process.

Comparing Energy Density

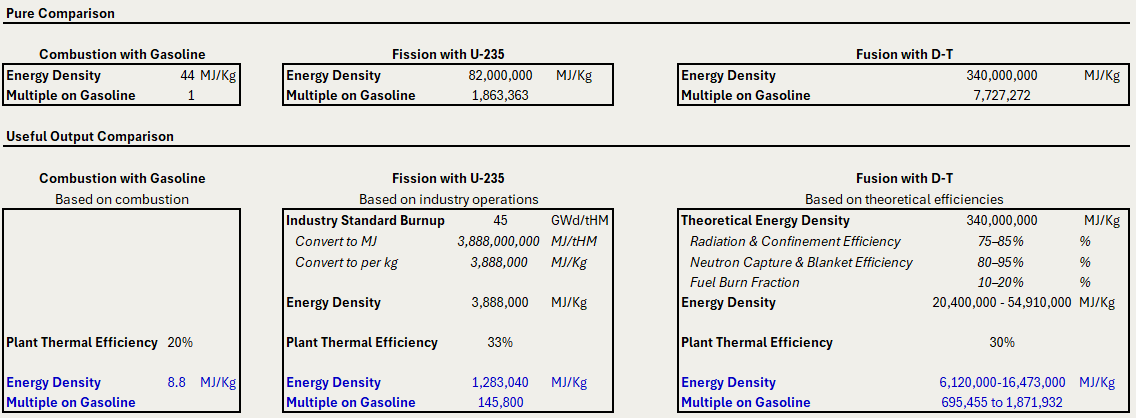
It's common to compare the energy densities of chemical, fission, and fusion reactions. Using the theoretical values above, fission and fusion are about 1.8 million and 7.7 million times more energy-dense than gasoline, respectively.

However, as mentioned, this comparison is misleading. Uranium isn't pure fissile U-235. Fusion has a variety of losses that may reduce the output. All three processes have inefficiencies when converting from thermal to electrical energy.

To conduct a more practical comparison, we establish the "useful" energy output from each reaction. To do this, we consider real-world constraints of fuel composition and system efficiencies.¹

• Gasoline Combustion: We account for a 20% efficiency in converting stored energy to practical work. This captures the thermal and mechanical losses commonly found in an automobile.

• U-235 Fission: We account for an industry standard fuel burnup value of 45 GWd/tHM, which is a measure of energy produced per input fuel mass. The units are GigaWatt-days per ton of heavy metal (U-235, U-238, plutonium, etc.). This metric is helpful as it inherently accounts for enrichment. We also assume 33% efficiency in thermal to electrical energy conversion.

• D-T Fusion: Since commercial fusion has not yet been achieved, we use illustrative assumptions. Our assumed efficiencies are 75% to 85% for radiation and confinement, 80% to 95% for neutron capture. Additionally, we assume 10% to 20% of input fuel is consumed (recognizing that unburned fuel can be recycled through the reactor multiple times). The fusion assumptions should be considered the least mature of the inputs.

Given this approach, we get the following adjusted values for energy density.

On a practical basis, when compared to gasoline,

• Fission is approximately 145,000 times more energy-dense

• Fusion is between 695,000 and 1,870,000 times more energy-dense

While lower than the theoretical numbers, these energy densities remain astounding.

However, perhaps the best comparison is a simple anecdotal example. While naval reactor specifications are classified, the enriched uranium core is estimated to be in the thousands of pounds. This powers an aircraft carrier for twenty-five years between refueling. By comparison, a large container ship burns 3-6 million pounds of fuel oil in just a two-week crossing of the Pacific.

Decay: Nature's Nuclear Transformation

Unlike fission and fusion, nuclear decay commonly occurs on Earth. When a nucleus is unstable (i.e., has the wrong ratio of protons to neutrons, or is too heavy), it will eventually decay through one of three processes. These release particles or radiation and often transform the nucleus into a completely different element.

Nuclear decay doesn't play a significant role in energy production, but it is central to radiation safety, waste management, medical imaging, and overall nuclear stability.

Decay also powers some of our most ambitious space missions through radioisotope thermoelectric generators (RTGs), more commonly referred to as "nuclear batteries." These units directly convert heat from radioactive decay into electricity. For example, the Voyager spacecraft used plutonium decay to transmit data to Earth from billions of miles away.

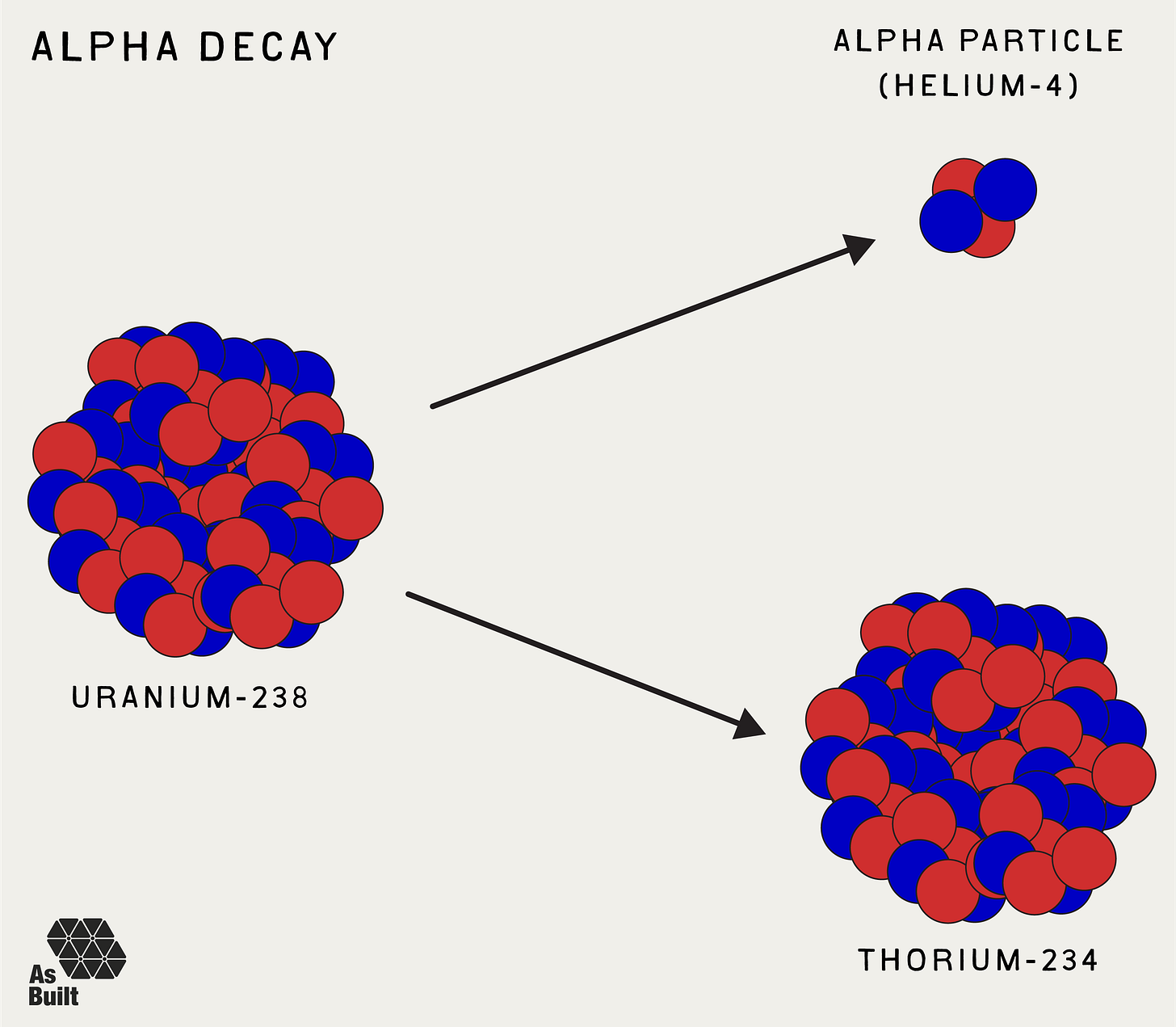
Alpha Decay (α)

In alpha decay, an unstable nucleus emits an alpha particle, which is made of two protons and two neutrons. Essentially, it is a helium-4 nucleus. This reduces the original atom's mass number by four and its atomic number by two, turning it into a different element. Alpha decay typically occurs in very heavy elements, such as uranium or radium, which are too large to remain stable.

Alpha particles have low penetration power and can be stopped by something as thin as a sheet of paper. However, they pose a significant health risk if inhaled or ingested.

Beta Decay (β)

Beta decay involves a change in the internal structure of a nucleus, where a neutron turns into a proton or vice versa. In beta-minus decay, a neutron converts to a proton, releasing an electron (beta particle) and an antineutrino. In beta-plus decay, which is a rarer process, a proton is converted into a neutron, accompanied by the emission of a positron and a neutrino.

This process changes the element by shifting the atomic number up or down by one. Beta particles have greater penetrating power than alpha particles and require thicker shielding, like plastic or glass, to stop them.

Gamma Decay (γ)

Gamma decay doesn't change the number of protons or neutrons. Instead, the nucleus releases excess energy in the form of light photons. Gamma decay often follows alpha or beta decay, as the nucleus rearranges into a more stable energy state. Because gamma rays are highly penetrating, they require dense shielding materials, such as lead or concrete, to contain them.

Half-Life

The half-life of a radioactive isotope is the time it takes for half of the sample to decay. Some isotopes have a short half-life and rapidly decay over seconds or minutes. Others have a long half-life and might take thousands or millions of years to decay.

A few example half-lives are:

• Hydrogen-3 (Tritium): 12.32 years

• Carbon-14: 5,730 years

• Uranium-238: 4.5 billion years

Decay matters for a wide range of applications. In medicine, certain isotopes are used in cancer therapy and diagnostic imaging. As mentioned earlier, carbon-14 decay is used to estimate the age of ancient organic materials.

In nuclear power generation, the half-lives of fission products define the duration for which nuclear waste remains hazardous. Additionally, heat from decay products continues even after reactor shutdown, which means active cooling is often needed both during and after operation. Managing this is a key factor in establishing passively safe nuclear reactors.

Tie Up

These physical laws have always held true, but our knowledge of them is remarkably new. Henry Becquerel discovered radioactivity from uranium salts in 1896, and Marie Curie famously furthered the research. Ernest Rutherford identified the atomic nucleus in 1911. James Chadwick discovered the neutron in 1932.

Just seven years later, in 1939, Leo Szilard and Albert Einstein wrote a letter to President Roosevelt warning that advances in nuclear fission made it probable this technology could be used for weapons, and that Nazi Germany might be developing such weapons. The Manhattan Project began three years later in 1942.

These three nuclear reactions now shape global power structures. Fission determines which nations can project naval force across oceans and which companies can provide carbon-free baseload power. Fusion could define the energy landscape of the next century. Decay governs nuclear waste policies and plant safety systems.

From here, the nuclear series will focus on fission. We’ll next examine how engineers harness fission to create sustained controlled chain reactions that enable electricity generation.

General References

Chemistry LibreTexts. "11.6: Bond Energy." Accessed May 23, 2025. https://chem.libretexts.org/Courses/WidenerUniversity/CHEM_175-General_Chemistry_I(Van_Bramer)/11:_Thermochemistry/11.06:_Bond_Energy.

Engineering Toolbox. "Fossil vs. Alternative Fuels - Energy Content." Accessed May 23, 2025. https://www.engineeringtoolbox.com/fossil-fuels-energy-content-d_1298.html.

OpenStax. "10.3: Nuclear Binding Energy." In University Physics III - Optics and Modern Physics (OpenStax). Accessed May 23, 2025. [https://phys.libretexts.org/Bookshelves/University_Physics/University_Physics_(OpenStax)/University_Physics_III_-_Optics_and_Modern_Physics

World Nuclear Association. "Physics of Uranium and Nuclear Energy." Accessed May 23, 2025. https://world-nuclear.org/information-library/nuclear-fuel-cycle/introduction/physics-of-nuclear-energy.

Peter Lux. "Energy Density of Uranium." PLUX. Accessed May 23, 2025. https://www.plux.co.uk/energy-density-of-uranium/.

World Nuclear Association. "Nuclear Fusion Power." Accessed May 23, 2025. https://world-nuclear.org/information-library/current-and-future-generation/nuclear-fusion-power.

Andlinger Center for Energy and the Environment. "Fusion Energy." Princeton University, 2016. https://acee.princeton.edu/wp-content/uploads/2016/05/ACEE-Fusion-Distillate.pdf.

International Atomic Energy Agency. "What is Deuterium?" Last modified January 13, 2023. Accessed May 23, 2025. https://www.iaea.org/newscenter/news/what-is-deuterium.

Richard J. Pearson. "The Availability & Supply of Critical Natural Resources for the Realization of a Fusion Pilot Plant: Fuels for Fusion." Presentation at U.S. DOE Fusion Workshop, Washington, DC, June 1–3, 2022.
https://science.osti.gov/-/media/fes/pdf/fes-presentations/2022/Pearson_resource-availability-and-supply_presentation.pdf.

NASA Science. "Power: Radioisotope Thermoelectric Generators." Accessed May 23, 2025. https://science.nasa.gov/planetary-science/programs/radioisotope-power-systems/power-radioisotope-thermoelectric-generators/.

ChemTalk. "Radioactive Decay | Alpha, Beta, and Gamma." Last modified October 11, 2024. Accessed May 23, 2025. https://chemistrytalk.org/radioactive-decay-alpha-beta-gamma/.

National Institute of Standards and Technology. "Atomic Masses and Fundamental Physical Constants." NIST Physical Measurement Laboratory, 2020. https://physics.nist.gov/cuu/Constants/f

Footnotes

1. Basic assumptions and calculations for “useful” energy density comparison.