Nuclear 02: How to Harness Fission
The tools that turn nuclear physics into controlled power
At 1:23:40 AM on April 26, 1986, operators at Chernobyl's Reactor 4 pressed the AZ-5 button, initiating an emergency SCRAM to shut down the unit. At the time, the reactor had been operating at about 200 MW, well below its nominal operating point. However, instead of shutting down, it surged.
Power is estimated to have hit 30,000 MW within seconds, but the true peak is unknown since instrumentation failed quickly. Driven by a control rod design flaw and a powerful positive feedback loop, this spike initiated one of the most infamous nuclear accidents in history.
To understand why this happened, we follow the neutron — the invisible particle that determines whether reactors generate power or catastrophe. In doing this, we'll look at how engineers harness nuclear fission, making the process self-sustaining and energy-generating, while also safe and controllable.
This piece builds on How nuclear physics works. Check it out if anything is unfamiliar.
Following the Neutron
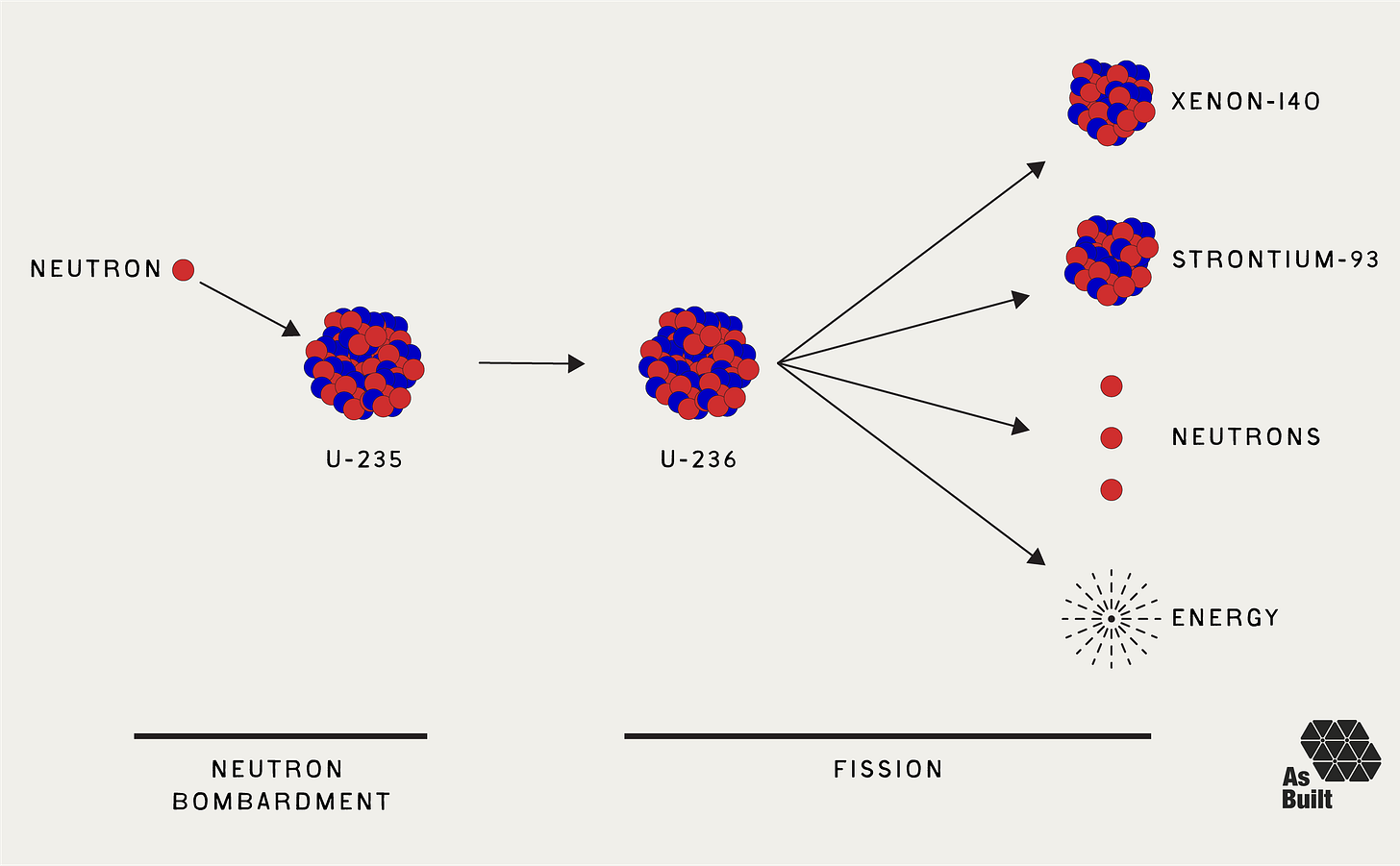
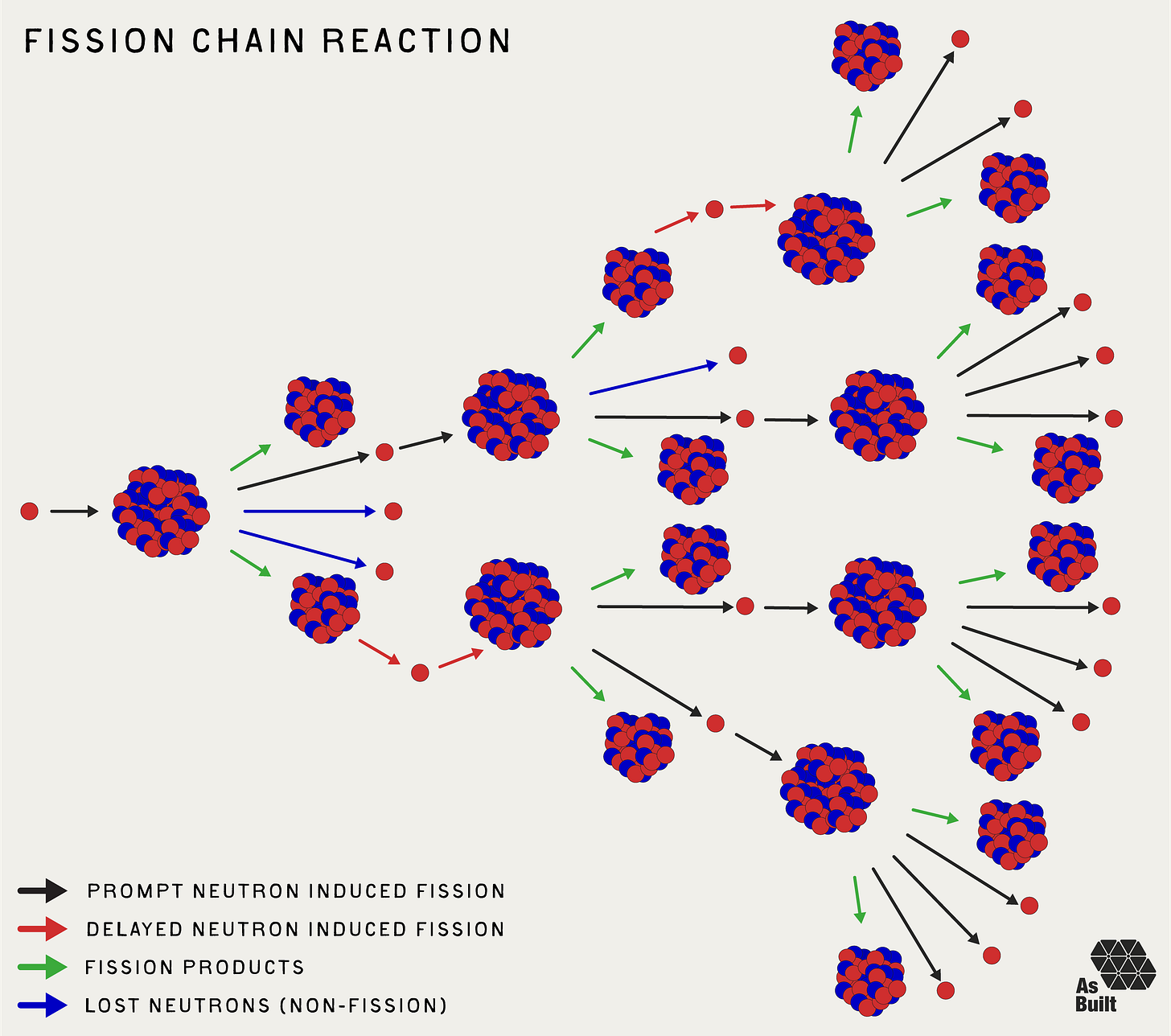
Recall from our last piece on nuclear physics that during fission, a uranium atom splits into smaller nuclei, releasing enormous energy and 2-3 new neutrons. While impressive, a single fission event is not enough to generate meaningful energy. We need trillions of fission events to occur every second. We achieve this by using the neutrons from one fission to initiate more. But there can't be too many. Otherwise, the chain reaction could run away, which is what happens in a meltdown or a bomb.
Unfortunately, we can't control individual neutrons. They're too small, too fast, and too numerous. Instead, we control their environment. By choosing the right materials and geometry they encounter, we can tip the odds, making fission more likely here or absorption more likely there. This approach forms the basis of modern reactor engineering.
Neutron Strikes
Our primary point of influence is when a neutron collides with an atom. Once released during fission, neutrons race through any material in their path — fuel, coolant, and reactor structure. Eventually, they collide with the atomic nuclei of these materials.
When a neutron strikes an atom, one of three things happens: it bounces off (scattering), gets captured (absorption), or splits the atom (fission).
Scattering can take two forms:
Elastic scattering conserves the total kinetic energy while redistributing it between particles. A collision with a small nucleus, like hydrogen, can stop a neutron completely. Impacts with larger nuclei slow them down much less. For this reason, light atoms like hydrogen serve as good neutron moderators, slowing them down.
Inelastic scattering occurs when fast neutrons carry enough energy to excite the nuclei of heavy atoms. The neutron loses kinetic energy by lifting the nucleus to a higher energy state. The excited nucleus then emits gamma rays to return to the ground state, therefore converting the neutron's motion into radiation.
Absorption permanently captures the neutron. The nucleus becomes heavier by one neutron and often releases gamma rays to shed excess energy. For example, when uranium-238 absorbs a neutron, it transforms into uranium-239, initiating a decay chain that ultimately produces plutonium-239.
Fission is a special type of absorption. The captured neutron tips a delicately balanced nucleus past its breaking point. Uranium-235 absorbs a neutron to become uranium-236, but this heavier nucleus is unstable. It splits violently into two fragments, ejecting 2-3 new neutrons and releasing 200 MeV of energy.
These interactions occur probabilistically. Every collision has some chance of each outcome, and the two biggest influencers are the target material and the neutron's energy at the point of collision.
Measuring Probability: Cross-Sections
To control these collisions, we first need a way to characterize their probabilities. To do this, we use a metric called cross-section. This isn't necessarily a measure of physical area, but a representation of the likelihood of an interaction occurring. It's an effective target area. If nuclei were dartboards, cross-sections would measure how big they appear to incoming neutrons.
Each type of interaction has its cross-section:
Scattering: the chance of bouncing off
Absorption: the chance of being captured
Fission: the chance of splitting the nucleus
We measure these phantom targets in units of barns. A barn is equivalent to 10^-28 square meters or roughly the size of a uranium nucleus. The unit's name comes from physicists' surprise at discovering certain cross-sections so large they were "as easy as hitting the broad side of a barn."
Some interactions are indeed that easy: with a 30,000-barn absorption cross-section, cadmium-113 voraciously captures thermal neutrons, making it ideal for use in control rods.
The cross-sections don't just depend on the target material. They shift dramatically with neutron speed, turning the same nucleus from nearly invisible to unmissable.
The Speed of Neutrons
Neutron speed and energy are directly related, and we generally categorize neutrons by their energy levels as:
Fast Neutrons: above 100 keV
Epithermal Neutrons: 0.1 eV to 100 keV
Thermal Neutrons: below 0.1 eV
When a neutron is first released from fission, it has about 2 MeV of energy and is moving at about 7% of the speed of light. This makes it a fast neutron. At those speeds, the probability of fission with most relevant materials is low.
However, as the neutron impacts many different atoms, it quickly loses energy through elastic scattering. After a few dozen collisions, the neutron has lost most of its initial kinetic energy and reaches thermal equilibrium with its surroundings.
In other words, it has about the same energy as the surrounding atoms due to their random thermal motion. At room temperature, this is about 0.025 eV. When the neutron hits this point, we consider it a thermal neutron.
Thermal neutrons behave dramatically differently. For example, uranium-235's fission cross sections are:
1.3 barns for fast neutrons
585 barns for thermal neutrons
This means that a thermal neutron is 450 times more likely to induce fission in U-235 than a fast neutron.
The process of slowing a neutron down is known as moderation, and is a cornerstone of reactor engineering. Materials like water and graphite are great moderators, since they contain light elements — hydrogen, carbon, oxygen — that collect neutron energy during elastic collisions.
Yet even with perfect moderation, controlling a chain reaction would be impossible without a unique quirk of nuclear physics: not all neutrons appear at once after a fission event.
The Time Delay That Saves Us
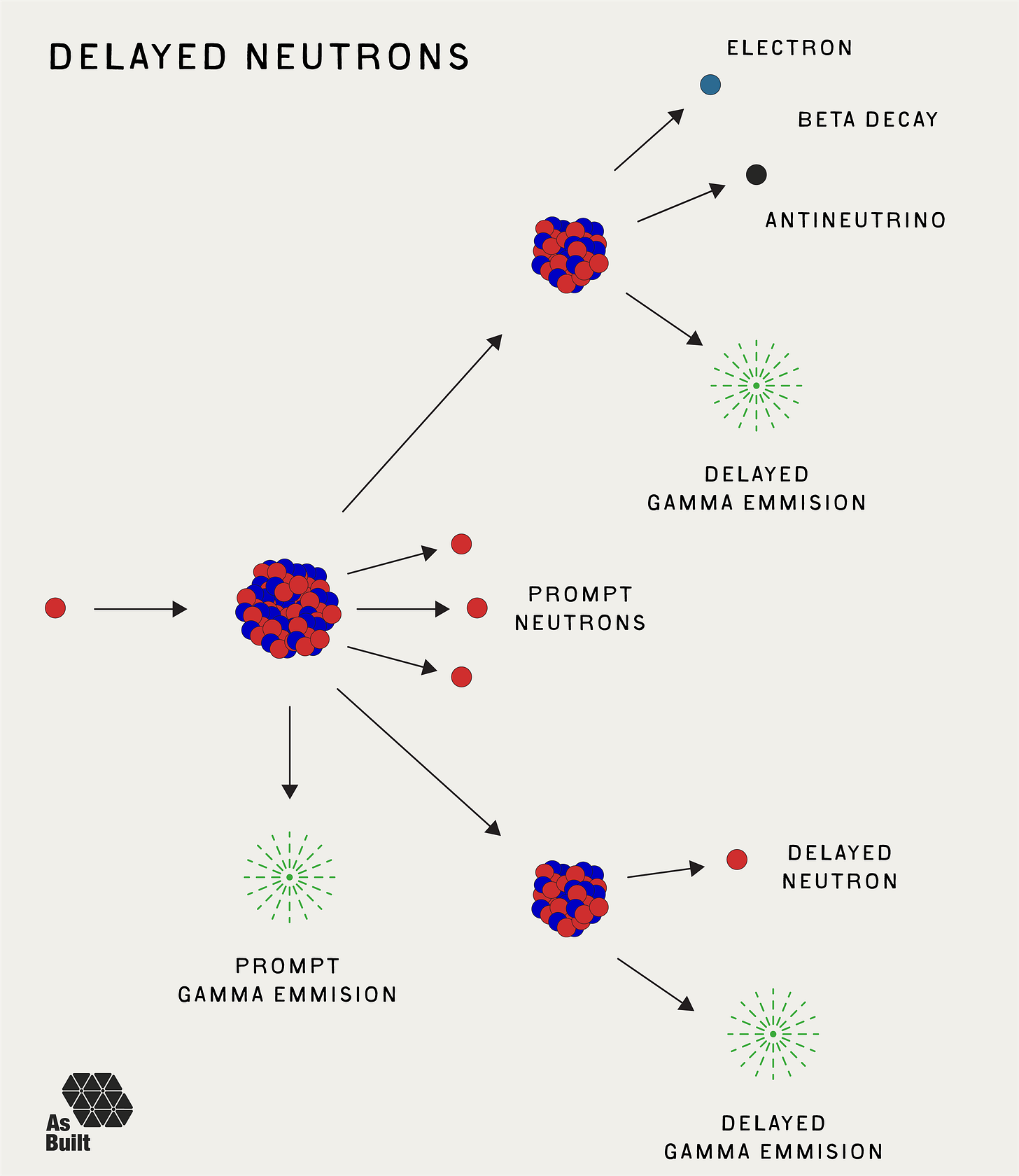
When a uranium atom splits by fission, about 99.3% of neutrons appear almost instantly (within nanoseconds) and are called prompt neutrons. The remaining 0.7% are known as delayed neutrons and are released a few milliseconds to a few minutes later. They come from the decay of certain fission products.
This small fraction of delayed neutrons is crucial for reactor control. Without them, the timescale from neutron-induced fission to a new batch of neutrons would be extremely short. Small increases in neutron quantity could cause reactor power to increase exponentially on a microsecond timescale, which is too fast to reasonably control with mechanical systems.
Delayed neutrons stretch that timescale from microseconds to tenths of a second. This is within the response time of modern control systems, giving operators time to adjust control rods and manage the changing reaction.
Criticality
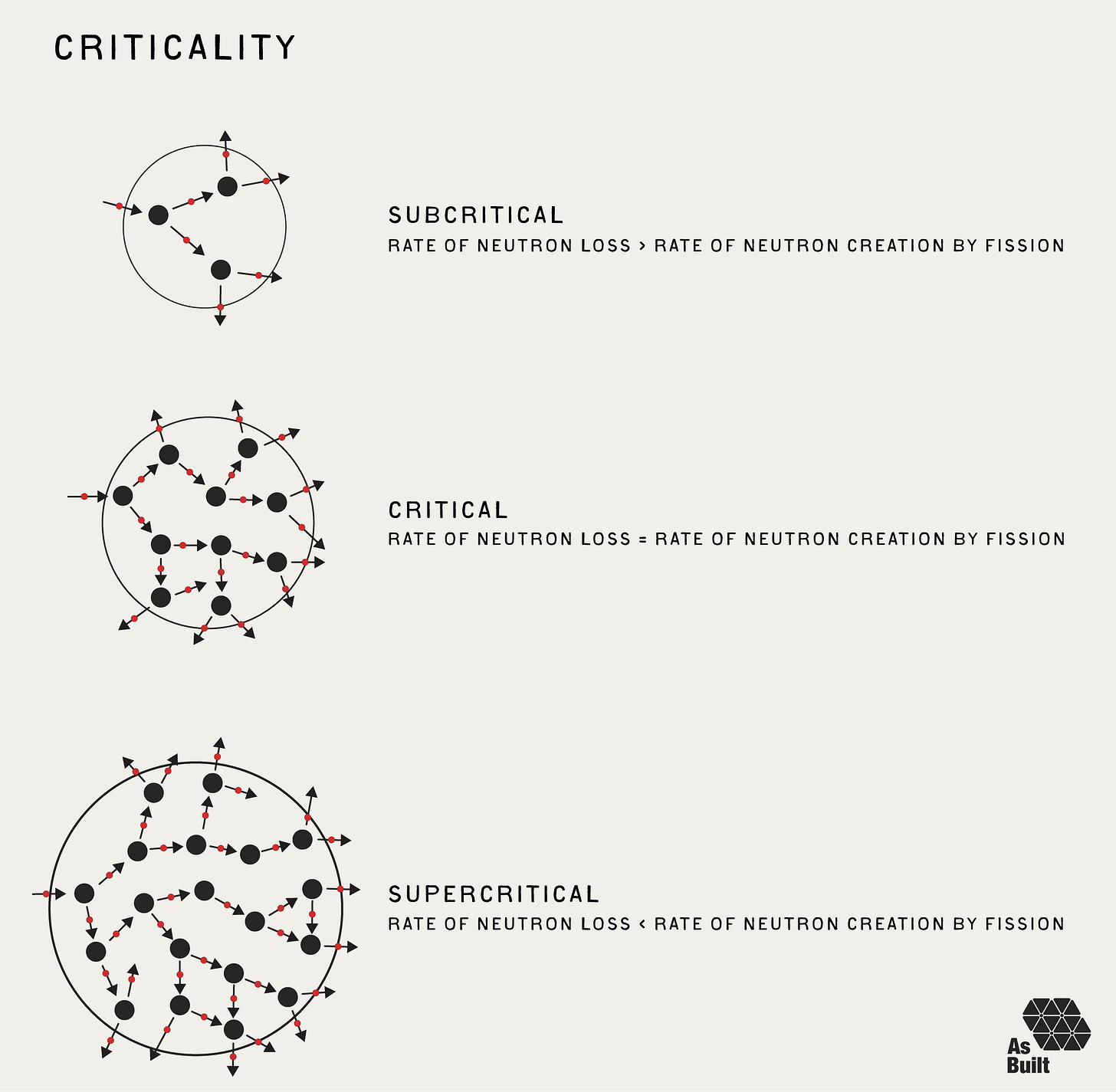
If we combine all the neutron factors covered so far, we can achieve the most fundamental balance in a reactor: criticality. This is the point at which a fission chain reaction is self-sustaining.
Consider a uranium-235 fission that releases three neutrons. If all three go on to induce additional fissions, the reaction accelerates. One fission causes three fissions. If none cause additional fissions, then the reaction dies out. One fission causes zero fissions.
The sweet spot is exactly one neutron induces one new fission. The other two neutrons get absorbed or escape. One fission causes one fission, creating the perfect balance of criticality.
We use this threshold to characterize the reactor's operating state and describe whether the neutron population is stable, growing, or shrinking:
Subcritical: Each fission leads to less than one additional fission. The reaction diminishes and eventually stops.
Critical: Each fission event leads to exactly one more fission event. The reactor maintains steady power.
Supercritical: Each fission leads to more than one additional fission. Power increases.
Critical and Prompt Critical
Generally, criticality is considered to include both the prompt and delayed neutrons. Alternatively, if only prompt neutrons sustained the chain reaction, then it is called prompt critical. Such a scenario can be uncontrollable. The prompt neutrons would sustain the reaction, and every additional delayed neutron that presented would further increase power levels.
For example, consider a system with 1,000 total neutrons, comprised of 993 prompt and 7 delayed neutrons.
If all 1000 neutrons are required to sustain the chain reaction, then the system is critical.
If only the 993 prompt neutrons are needed, then the system is prompt critical.
Nearly all reactors are designed to operate with delayed neutrons factored in. Weapons, on the other hand, do not. They typically rely on prompt neutrons alone for their explosive power release.
Reactivity
One challenge with criticality is that it's difficult to measure it directly. Instead, we use the concept of reactivity to characterize how far a reactor is from criticality.
First, let's think of neutrons in generations. Each generation is born and either creates another generation or is lost to the system. By comparing one generation to the next, we can determine whether the neutron population is growing, shrinking, or staying constant.
We use the neutron multiplication factor, k-effective (keff), to make this comparison.
This measurement is centered around 1, which is the threshold for reactor behavior:
keff < 1: Subcritical (power falling)
keff = 1: Critical (power steady)
keff > 1: Supercritical (power rising)
Next, we rearrange the equation to magnify changes and define reactivity as:
This approach centers reactivity around zero:
ρ<0: Negative reactivity, fewer neutrons in each generation, power falling
ρ=0: Zero reactivity, steady neutron population, reactor critical
ρ>0: Positive reactivity, more neutrons in each generation, power rising
Dollars and Cents
Although reactivity is dimensionless, scientists use various units to reference it. In the US, reactivity is often measured in dollars and cents. One dollar of reactivity is the amount between normal criticality and prompt criticality. A cent is one-hundredth of a dollar. At zero cents, we're critical. At 100 cents (one dollar), we're prompt critical.
< 0$: Reactor is subcritical
= 0$: Reactor is critical, using both prompt and delayed neutrons (typical steady state operation)
0$ to 1$: Reactor is supercritical, but still depends on delayed neutrons, and power rise is slow enough to be safely controlled
= 1$: Reactor is prompt critical, and power increases faster than conventional control mechanisms can respond
Every action affects reactivity. Insert control rods: negative. Add fuel: positive. Increase temperature: negative (in properly designed reactors).
With these fundamental concepts, we can now understand how engineers select materials and design reactors.
Engineering a Reactor
In designing a reactor, the core objective is to achieve and control criticality. However, there are many solutions to this problem. Each comes from a different combination of architectural, design, and operational decisions. The choices have significant path dependency, and all must be considered in unison as the reactor is scoped.
Thermal vs. Fast Architecture
The top-most decision is whether the reactor operates in the fast or thermal regime. So far, we've highlighted the need to moderate neutrons to thermal energies, but reactors can also be built to operate with fast neutrons.
Known as fast reactors, these plants are designed to work with unmoderated fast neutrons. Since fission cross sections are smaller with fast neutrons, these plants require more highly enriched uranium (15-20% or more) or plutonium-based fuel.
The approach brings compelling advantages. Fast reactors breed more fuel than they consume by converting U-238 to plutonium. Their higher energy density enables smaller cores, while liquid metal coolants allow high-temperature operation without pressurization.
Yet fast reactors remain rare commercially. Sodium coolant burns on contact with air and reacts violently with water. Higher enrichment raises proliferation concerns. High construction costs have limited adoption.
Fuel Considerations
Fission reactors can be powered by uranium and plutonium, while thorium can also be used indirectly as a fuel.
Uranium
Uranium is the most common fission fuel. It is a naturally occurring resource and typically found as 99.3% uranium-238 and 0.07% uranium-235. Of these isotopes, only uranium-235 is fissile and can be used for fission. Some reactors are engineered to operate with natural uranium and low concentrations of uranium-235.
However, most require a higher concentration of fissile uranium-235. The process of enrichment increases the relative concentration of uranium-235 atoms to those of uranium-238. Commercial reactors commonly use 3-5% enriched uranium, but advanced designs consider levels up to 20%.
Plutonium
For all practical purposes, plutonium is not a naturally occurring element. Instead, it's created as a byproduct inside uranium reactors. Uranium-238 absorbs a neutron and becomes uranium-239, which is unstable. It undergoes beta decay, transforming into neptunium-239, which is also unstable. After one more beta decay, plutonium-239 emerges. This process happens anytime uranium-238 is exposed to neutrons, which occurs in all commercial reactors.
U-238 + neutron -> U-239 -> Np-239 + beta emission -> Pu-239 + beta emission
Interestingly, plutonium itself is fissionable. Therefore, a reactor begins burning pure uranium and gradually transitions to a mixture of uranium and plutonium. The breeding is significant. Though no plutonium is loaded initially, by the end of a fuel cycle, it contributes roughly one-third of the total energy output.
Plutonium-239 is an exceptional reactor fuel. Its thermal fission cross-section is 750 barns—even higher than uranium-235's 585 barns—and it requires a smaller critical mass. These same properties, however, make it suitable for nuclear weapons, creating a proliferation risk.
Thorium
Thorium has long been contemplated as an alternate nuclear fuel. Thorium-232 can breed into fissile uranium-233, which has a 530-barn cross-section, rivaling that of uranium-235. However, the process also creates uranium-232, which emits fierce gamma radiation. This makes fuel handling particularly hazardous.
Thorium is attractive due to its abundance, which is approximately three times that of uranium. However, while several countries pursue thorium research, only India has made it central to their nuclear strategy.
Fuel Mass, Shape, and Enrichment
Once a fuel is selected, mass and geometry influence how many neutrons stay inside the core versus escaping. A sphere minimizes surface area and is the most efficient at retaining neutrons. Depending on the shape, a certain amount of mass is required. Below critical mass, too many neutrons flee before causing fissions, and the chain reaction cannot sustain itself.
Additionally, in the case of uranium, the enrichment level determines the number of fissile targets. By increasing the concentration of uranium-235 targets through enrichment, fission probabilities can be improved.
Operational Factors
Beyond design, specific passive and active operational considerations also influence criticality. Temperature can provide inherent safety. Most modern reactors have a negative temperature coefficient of reactivity, meaning that rising temperature naturally reduces the rate of fission. This is a deliberate strategy to prevent runaway reactions. This is achieved through mechanisms such as:
Doppler Broadening: As fuel temperature rises, uranium-238 nuclei vibrate more vigorously. This broadens their neutron absorption resonances, increasing the likelihood that they will capture neutrons instead of allowing them to cause fission. The effect is instantaneous — occurring in microseconds — and acts as the first, fastest line of defense against sudden power surges.
Void Formation: In thermal reactors that use water as a moderator, higher temperatures reduce water density, creating steam bubbles (voids). Steam is far less effective at slowing down neutrons than liquid water, resulting in fewer neutrons in the thermal energy range, which in turn reduces the fission rate. This feedback is critical in boiling water reactors and pressurized water reactors, but does not occur in gas-cooled reactors or liquid sodium fast reactors.
Thermal Expansion: As the fuel and core structures heat up, the atoms move farther apart, slightly reducing fuel density and increasing neutron leakage. This decreases the probability of neutron–fuel interactions that cause fission. While slower than Doppler broadening — acting over seconds rather than microseconds — it provides an additional layer of stabilizing feedback.
These negative feedback mechanisms create inherent stability. If a reactor begins to overheat, physics itself applies the brakes—no control rods, no operators, no power required. This self-regulating behavior underpins modern reactor safety.
Chernobyl’s RBMK design violated this principle catastrophically. Unlike water-moderated reactors, the RBMK used graphite for moderation and water primarily as coolant and neutron absorber. When water boiled into steam, its ability to absorb neutrons decreased, while graphite continued moderating. This left more neutrons available for the chain reaction, increasing reactivity — a positive void coefficient. Under the unstable conditions during the accident, rising power produced more steam, which in turn increased power further, creating a runaway feedback loop. Within seconds, this led to a massive steam explosion and subsequent core destruction.
For active control, we use control rods. These are made from neutron-hungry materials like boron or cadmium; they're inserted to absorb excess neutrons or withdrawn to increase reactivity. They're the throttle and brake of nuclear reactions, giving operators direct plant control.
Selecting Materials
Lastly, we must pick the materials we use throughout the plant. Since our primary method of controlling neutrons involves collisions, the type of material they impact determines everything. Looking at the problem through this lens, we can use the various cross-sections to consider which materials are best for which role.
Fissile fuels have large fission cross-sections for sustained chain reactions, such as uranium-235 and plutonium-239.
Fertile materials absorb neutrons without fissioning and instead breed new fissile isotopes. Uranium-238 can capture a neutron to create plutonium-239 while leaving enough neutrons for the chain reaction.
Control materials feature enormous absorption cross-sections. Examples include cadmium and boron. Natural boron's 3,840-barn absorption cross-section makes it ideal for control rods and emergency shutdown.
Structural materials must have minimal absorption to avoid influencing the nuclear reactor. Zirconium is nearly transparent to neutrons, perfect for cladding for fuel rods without changing the reaction dynamics.
Moderators combine high scattering with low absorption. We want to slow a neutron down, but not capture any. Water, heavy water, and graphite are all effective moderators. Water's hydrogen atoms have a scattering cross section of 20 barns, but an absorption cross section of only 0.33 barns. They slow down neutrons with minimal losses.
Coolants vary by reactor type. Water often serves dual purposes in thermal reactors as both moderator and coolant. In fast reactors, sodium and lead are best as they have low absorption and no moderation.
Harnessing the Neutron
Ultimately, nuclear reactors come down to controlling neutrons, which is an exercise in exposing them to the right materials at the right times. As we saw in the last piece, the nuclear fission reaction enables the release of immense energy by splitting atoms. The strategies outlined in this piece represent the ways we can harness, control, and sustain this phenomenon. They're the tools in the toolkit of a reactor designer.
In the following piece, we'll examine the various types of reactors that can be created using these tools. We'll see radically different reactor designs. Pressurized water reactors combine moderators and coolants into one fluid. CANDU plants use heavy water to burn natural uranium without enrichment, while fast reactors can breed fuel for other reactors.
While the core physics always remain the same, this toolkit enables a variety of different goals to be achieved by reactor designers around the world.
General References
Benedict, Manson, Thomas H. Pigford, and Hans Wolfgang Levi. Nuclear Chemical Engineering. 2nd ed. New York: McGraw-Hill, 1981.
Bickel, John H. "Module 3: Neutron Induced Reactions." Department of Nuclear Engineering, North Carolina State University, 2012. https://www.nrc.gov/docs/ML1214/ML12142A051.pdf.
International Atomic Energy Agency. INSAG-7: The Chernobyl Accident: Updating of INSAG-1. Vienna: IAEA, 1992. https://www-pub.iaea.org/MTCD/Publications/PDF/Pub913e_web.pdf
International Atomic Energy Agency. Thorium Fuel Cycle — Potential Benefits and Challenges. IAEA-TECDOC-1450. Vienna: IAEA, 2005. https://www-pub.iaea.org/MTCD/Publications/PDF/TE_1450_web.pdf
Keepin, G. R. Physics of Nuclear Kinetics. Reading, MA: Addison-Wesley, 1965.
Knoll, Glenn F. Radiation Detection and Measurement. 4th ed. Hoboken, NJ: John Wiley & Sons, 2010.
Lamarsh, John R., and Anthony J. Baratta. Introduction to Nuclear Engineering. 3rd ed. Upper Saddle River, NJ: Prentice Hall, 2001.
National Nuclear Data Center. "Chart of Nuclides." Brookhaven National Laboratory. Accessed August 2025. https://www.nndc.bnl.gov/chart/.
OECD Nuclear Energy Agency. Technology Roadmap Update for Generation IV Nuclear Energy Systems. Paris: OECD-NEA, 2014. https://www.gen-4.org/gif/upload/docs/application/pdf/2014-03/gif-tru2014.pdf
Stacey, Weston M. Nuclear Reactor Physics. 3rd ed. Weinheim: Wiley-VCH, 2018.
Tucker, Colin. How to Drive a Nuclear Reactor. Cham: Springer International Publishing, 2020.
World Nuclear Association. "Fast Neutron Reactors." Last modified March 2024. https://world-nuclear.org/information-library/current-and-future-generation/fast-neutron-reactors.aspx.
World Nuclear Association. "Physics of Uranium and Nuclear Energy." Accessed May 2025. https://world-nuclear.org/information-library/nuclear-fuel-cycle/introduction/physics-of-nuclear-energy.
World Nuclear Association. "Plutonium." Last modified August 16, 2023. https://world-nuclear.org/information-library/nuclear-fuel-cycle/fuel-recycling/plutonium.